动态规划总结-买卖股票最佳时机

买卖股票的最佳时机，买卖股票的最佳时机II，买卖股票的最佳时机含手续费前三道题循循渐进，可在一起总结

买卖股票的最佳时机III，买卖股票的最佳时机IV 可在一起总结

最佳买卖股票时机含冷冻期比较难理解，可以单独总结

买卖股票的最佳时机

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。你只能选择某一天买入这只股票，并选择在未来的某一个不同的日子卖出该股票。设计一个算法来计算你所能获取的最大利润。返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。

示例：输入：[7,1,5,3,6,4]，输出：5（在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 ）

输入：prices = [7,6,4,3,1]，输出：0，解释：在这种情况下, 没有交易完成, 所以最大利润为 0

dp[i][0] 表示第i天持有股票所得最多现金，一开始现金是0，那么加入第i天买入股票现金就是 -prices[i]，这是一个负数
dp[i][1] 表示第i天不持有股票所得最多现金。注意这里说的是“持有”，“持有”不代表就是当天“买入”！也有可能是昨天就买入了，今天保持持有的状态
第i天持有股票即dp[i][0]，那么可以由两个状态推出来
- 第i-1天就持有股票，那么就保持现状，所得现金就是昨天持有股票的所得现金即：dp[i - 1][0]
- 第i天买入股票，所得现金就是买入今天的股票后所得现金即：-prices[i]
dp[i][0] 应该选所得现金最大的，所以dp[i][0] = max(dp[i - 1][0], -prices[i])
第i天不持有股票即dp[i][1]，也可以由两个状态推出来
- 第i-1天就不持有股票，那么就保持现状，所得现金就是昨天不持有股票的所得现金即：dp[i - 1][1]
- 第i天卖出股票，所得现金就是按照今天股票价格卖出后所得现金即：prices[i] + dp[i - 1][0]
同样dp[i][1]取最大的，dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i - 1][0])

dp[0][0] 表示第0天持有股票，此时的持有股票就一定是买入股票了，因为不可能有前一天推出来，所以dp[0][0] -= prices[0]
dp[0][1]表示第0天不持有股票，不持有股票那么现金就是0，所以dp[0][1] = 0
从递推公式可以看出dp[i]都是由dp[i - 1]推导出来的，那么一定是从前向后遍历

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        length = len(prices)
        if len == 0:
            return 0
        # dp[i][0]代表第i天持有股票的最大收益
        # dp[i][1]代表第i天不持有股票的最大收益
        dp = [[0] * 2 for _ in range(length)]
        dp[0][0] = -prices[0]  # 第一天持有，那肯定是买入
        dp[0][1] = 0           # 第一天未持有
        for i in range(1, length):
            dp[i][0] = max(dp[i-1][0], -prices[i])  # 计算每天持有股票的最大金额
            dp[i][1] = max(dp[i-1][1], prices[i] + dp[i-1][0])  # 计算每天不持有股票的最大金额
        return dp[-1][1]

买卖股票的最佳时机II

给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易（多次买卖一支股票）。注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例1: 输入: [7,1,5,3,6,4]，输出: 7，解释：5-1 = 4，6-3 = 3 ，4+3=7

示例 2: 输入: [1,2,3,4,5]，输出: 4，5-1 = 4

本题和上一题的唯一区别是本题股票可以买卖多次了（注意只有一只股票，所以再次购买前要出售掉之前的股票）
dp[i][0] 表示第i天持有股票所得现金。dp[i][1]表示第i天不持有股票所得最多现金
第i天持有股票即dp[i][0]，那么可以由两个状态推出来
- 第i-1天就持有股票，那么就保持现状，所得现金就是昨天持有股票的所得现金即：dp[i - 1][0]
- 第i天买入股票，所得现金就是昨天不持有股票的所得现金减去今天的股票价格即：dp[i - 1][1] - prices[i]。这里是和上一题唯一不同的地方，因为上一题股票全程只能买卖一次，所以如果买入股票，那么第i天持有股票即dp[i][0] 一定就是 -prices[i]。而本题，因为一只股票可以买卖多次，所以当第i天买入股票的时候，所持有的现金可能有之前买卖过的利润。
第i天不持有股票即 dp[i][1] 的情况，依然可以由两个状态推出来
- 第i-1天就不持有股票，那么就保持现状，所得现金就是昨天不持有股票的所得现金即：dp[i - 1][1]
- 第i天卖出股票，所得现金就是按照今天股票价格卖出后所得现金即：prices[i] + dp[i - 1][0]

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        length = len(prices)
        dp = [[0] * 2 for _ in range(length)]
        dp[0][0] = -prices[0]
        dp[0][1] = 0
        for i in range(1, length):
            dp[i][0] = max(dp[i-1][0], dp[i-1][1] - prices[i]) #注意这里是和121. 买卖股票的最佳时机唯一不同的地方
            dp[i][1] = max(dp[i-1][1], dp[i-1][0] + prices[i])
        return dp[-1][1]

买卖股票的最佳时机含手续费

给定一个整数数组 prices，其中第 i 个元素代表了第 i 天的股票价格；非负整数 fee 代表了交易股票的手续费用。你可以无限次地完成交易，但是你每笔交易都需要付手续费。如果你已经购买了一个股票，在卖出它之前你就不能再继续购买股票了。返回获得利润的最大值。注意：这里的一笔交易指买入持有并卖出股票的整个过程，每笔交易你只需要为支付一次手续费。

示例 1，输入: prices = [1, 3, 2, 8, 4, 9], fee = 2，输出: 8

解释: 能够达到的最大利润:

在此处买入 prices[0] = 1
在此处卖出 prices[3] = 8
在此处买入 prices[4] = 4
在此处卖出 prices[5] = 9
总利润: ((8 - 1) - 2) + ((9 - 4) - 2) = 8

相对于买卖股票的最佳时机II，本题只需要在计算卖出操作的时候减去手续费就可以了，代码几乎是一样的。

dp[i][0] 表示第i天持有股票所省最多现金。 dp[i][1]表示第i天不持有股票所得最多现金
第i天持有股票即dp[i][0]，那么可以由两个状态推出来
- 第i-1天就持有股票，那么就保持现状，所得现金就是昨天持有股票的所得现金即：dp[i - 1][0]
- 第i天买入股票，所得现金就是昨天不持有股票的所得现金减去今天的股票价格即：dp[i - 1][1] - prices[i]
- 所以：dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i])
第i天不持有股票即dp[i][1]的情况，依然可以由两个状态推出来
- 第i-1天就不持有股票，那么就保持现状，所得现金就是昨天不持有股票的所得现金即：dp[i - 1][1]
- 第i天卖出股票，所得现金就是按照今天股票价格卖出后所得现金，注意这里需要有手续费了即：dp[i - 1][0] + prices[i] - fee
- 所以：dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i] - fee)

class Solution:
    def maxProfit(self, prices: List[int], fee: int) -> int:
        n = len(prices)
        dp = [[0] * 2 for _ in range(n)]
        dp[0][0] = -prices[0] #持股票
        for i in range(1, n):
            dp[i][0] = max(dp[i-1][0], dp[i-1][1] - prices[i])
            dp[i][1] = max(dp[i-1][1], dp[i-1][0] + prices[i] - fee)  # 减去手续费
        return max(dp[-1][0], dp[-1][1])

买卖股票的最佳时机III

给定一个数组，它的第 i 个元素是一支给定的股票在第 i 天的价格。设计一个算法来计算你所能获取的最大利润。你最多可以完成两笔交易。注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例 1，输入：prices = [3,3,5,0,0,3,1,4]，输出：6，解释：在第 4 天（股票价格 = 0）的时候买入，在第 6 天（股票价格 = 3）的时候卖出，这笔交易所能获得利润 = 3-0 = 3 。随后，在第 7 天（股票价格 = 1）的时候买入，在第 8 天（股票价格 = 4）的时候卖出，这笔交易所能获得利润 = 4-1 = 3

示例 2：输入：prices = [1,2,3,4,5]，输出：4 解释：在第 1 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 5）的时候卖出, 这笔交易所能获得利润 = 5-1 = 4。注意你不能在第 1 天和第 2 天接连购买股票，之后再将它们卖出。因为这样属于同时参与了多笔交易，你必须在再次购买前出售掉之前的股票。

示例 3：输入：prices = [7,6,4,3,1]，输出：0 解释：在这个情况下, 没有交易完成, 所以最大利润为0

本题关键在于至多买卖两次，这意味着可以买卖一次，可以买卖两次，也可以不买卖
所有就有五个状态
- 1. 没有操作
- 1. 第一次持有股票
- 1. 第一次不持有股票
- 1. 第二次持有股票
- 1. 第二次不持有股票
dp[i][j] 中 i表示第i天，j为 [0 - 4] 五个状态，dp[i][j] 表示第i天状态j所剩最大现金
达到dp[i][1] 状态，有两个具体操作
- 第i天买入股票了，那么dp[i][1] = dp[i-1][0] - prices[i]
- 第i天没有操作，而是沿用前一天买入的状态，即：dp[i][1] = dp[i - 1][1]
- 取两种方式的最大值，dp[i][1] = max(dp[i-1][0] - prices[i], dp[i-1][1])
同理dp[i][2]也有两个操作
- 第i天卖出股票了，那么dp[i][2] = dp[i - 1][1] + prices[i]
- 第i天没有操作，沿用前一天卖出股票的状态，即：dp[i][2] = dp[i - 1][2]
- 同理取最大值，dp[i][2] = max(dp[i-1][1] + prices[i], dp[i-1][2])
同理可推出剩下状态部分：
- dp[i][3] = max(dp[i-1][3], dp[i-1][2] - prices[i])
- dp[i][4] = max(dp[i-1][4], dp[i-1][3] + prices[i])

初始化，第0天没有操作, 所以 dp[0][0] = 0
第0天做第一次买入的操作，dp[0][1] = -prices[0]
第0天做第一次卖出，还没有买入，所以没有卖出的金额，所以 dp[0][2] = 0
第0天第二次买入，初始值应该是多少呢？第二次买入依赖于第一次卖出的状态，其实相当于第0天第一次买入了，第一次卖出了，然后再买入一次（第二次买入），那么现在手头上没有现金，只要买入，现金就做相应的减少。所以第二次买入操作，初始化为：dp[0][3] = -prices[0]
同理第二次卖出初始化 dp[0][4] = 0

从递归公式其实已经可以看出，一定是从前向后遍历，因为dp[i]，依靠dp[i - 1]的数值

class Solution:
    def maxProfit(self, prices: List[int]) -> int:
        if len(prices) == 0:
            return 0
          
        dp = [[0] * 5 for _ in range(len(prices))]
        dp[0][1] = -prices[0]
        dp[0][3] = -prices[0]
        
        for i in range(1, len(prices)):
            dp[i][0] = dp[i-1][0]  # 这一步可以省略
            dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i])
            dp[i][2] = max(dp[i-1][2], dp[i-1][1] + prices[i])
            dp[i][3] = max(dp[i-1][3], dp[i-1][2] - prices[i])
            dp[i][4] = max(dp[i-1][4], dp[i-1][3] + prices[i])
        return dp[-1][4]

买卖股票的最佳时机IV

给定一个整数数组 prices ，它的第 i 个元素 prices[i] 是一支给定的股票在第 i 天的价格。设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例 1：输入：k = 2, prices = [2,4,1]，输出：2 解释：在第 1 天 (股票价格 = 2) 的时候买入，在第 2 天 (股票价格 = 4) 的时候卖出，这笔交易所能获得利润 = 4-2 = 2

示例 2：输入：k = 2, prices = [3,2,6,5,0,3]，输出：7 解释：在第 2 天 (股票价格 = 2) 的时候买入，在第 3 天 (股票价格 = 6) 的时候卖出, 这笔交易所能获得利润 = 6-2 = 4。随后，在第 5 天 (股票价格 = 0) 的时候买入，在第 6 天 (股票价格 = 3) 的时候卖出, 这笔交易所能获得利润 = 3-0 = 3

dp[i][j] ：第i天的状态为j，所剩下的最大现金是dp[i][j]
j的状态表示为：
- 0 表示不操作
- 1 第一次买入
- 2 第一次卖出
- 3 第二次买入
- 4 第二次卖出
除了0以外，偶数就是卖出，奇数就是买入, 题目要求是至多有K笔交易，那么j的范围就定义为 2 * k + 1 就可以了
达到 dp[i][1] 状态，有两个具体操作
- 操作一：第i天买入股票了，那么dp[i][1] = dp[i - 1][0] - prices[i]
- 操作二：第i天没有操作，而是沿用前一天买入的状态，即：dp[i][1] = dp[i - 1][1]
- 选最大的，所以 dp[i][1] = max(dp[i - 1][0] - prices[i], dp[i - 1][1])
同理dp[i][2]也有两个操作：
- 操作一：第i天卖出股票了，那么 dp[i][2] = dp[i - 1][1] + prices[i]
- 操作二：第i天没有操作，沿用前一天卖出股票的状态，即：dp[i][2] = dp[i - 1][2]
- 选最大的，所以 dp[i][2] = max(dp[i - 1][1] + prices[i], dp[i - 1][2])
本题和上一题最大的区别就是这里要类比j为奇数是买，偶数是卖的状态。
所以同理可以推出 dp[0][j] 当j为奇数的时候都初始化为 -prices[0]
递归公式其实已经可以看出，一定是从前向后遍历，因为dp[i]，依靠dp[i - 1]的数值

class Solution:
    def maxProfit(self, k: int, prices: List[int]) -> int:
        if len(prices) == 0:
            return 0
        
        dp = [[0] * (2*k+1) for _ in range(len(prices))] 
        
        # 当j为奇数的时候都初始化为 -prices[0]
        for j in range(1, 2*k, 2):
            dp[0][j] = -prices[0]
            
        for i in range(1, len(prices)):
            for j in range(0, 2*k-1, 2):
                dp[i][j+1] = max(dp[i-1][j+1], dp[i-1][j] - prices[i])  # 买入
                dp[i][j+2] = max(dp[i-1][j+2], dp[i-1][j+1] + prices[i])  # 卖出
        return dp[-1][2*k]

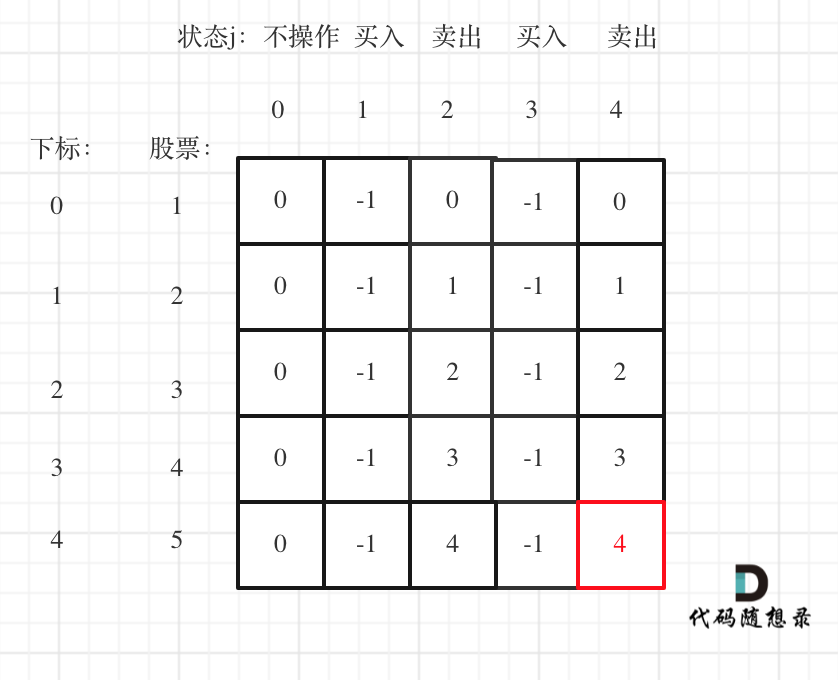
以输入[1,2,3,4,5]，k=2为例

最佳买卖股票时机含冷冻期

给定一个整数数组，其中第 i 个元素代表了第 i 天的股票价格。设计一个算法计算出最大利润。在满足以下约束条件下，你可以尽可能地完成更多的交易（多次买卖一支股票）:

你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。
卖出股票后，你无法在第二天买入股票 (即冷冻期为 1 天)。

示例: 输入: [1,2,3,0,2]，输出: 3，解释: 对应的交易状态为: [买入, 卖出, 冷冻期, 买入, 卖出]

dp[i][j] 表示第i天状态为j，所剩的最多现金为dp[i][j]
具体可以区分出如下四个状态
- 状态一：持有股票状态（今天买入股票，或者是之前就买入了股票然后没有操作，一直持有）
- 不持有股票状态，这里就有两种卖出股票状态
  - 状态二：保持卖出股票的状态（两天前就卖出了股票，度过一天冷冻期。或者是前一天就是卖出股票状态，一直没操作）
  - 状态三：今天卖出股票
- 状态四：今天为冷冻期状态，但冷冻期状态不可持续，只有一天

https://programmercarl.com/0309.%E6%9C%80%E4%BD%B3%E4%B9%B0%E5%8D%96%E8%82%A1%E7%A5%A8%E6%97%B6%E6%9C%BA%E5%90%AB%E5%86%B7%E5%86%BB%E6%9C%9F.html#%E6%80%9D%E8%B7%AF