星尘

单调栈

发表于 更新于 分类于 ，

每日温度

请根据每日 气温 列表，重新生成一个列表。对应位置的输出为：要想观测到更高的气温，至少需要等待的天数。如果气温在这之后都不会升高，请在该位置用 0 来代替。

例如，给定一个列表 temperatures = [73, 74, 75, 71, 69, 72, 76, 73]，你的输出应该是 [1, 1, 4, 2, 1, 1, 0, 0]。提示：气温 列表长度的范围是 [1, 30000]。每个气温的值的均为华氏度，都是在 [30, 100] 范围内的整数。

通常是一维数组，要寻找任一个元素的右边或者左边第一个比自己大或者小的元素的位置，此时我们就要想到可以用单调栈了。时间复杂度为O(n)

单调栈的本质是空间换时间，因为在遍历的过程中需要用一个栈来记录右边第一个比当前元素高的元素，优点是整个数组只需要遍历一次

更直白来说，就是用一个栈来记录我们遍历过的元素，因为我们遍历数组的时候，我们不知道之前都遍历了哪些元素，以至于遍历一个元素找不到是不是之前遍历过一个更小的，所以我们需要用一个容器（这里用单调栈）来记录我们遍历过的元素。

在使用单调栈的时候首先要明确如下几点：

  1. 单调栈里存放的元素是什么？

    • 单调栈里只需要存放元素的下标i就可以了，如果需要使用对应的元素，直接T[i]就可以获取。

  2. 单调栈里元素是递增呢？ 还是递减呢？

    • 顺序的描述为 从栈头到栈底的顺序，如果是求右边第一个比自己大的元素，那么就是单调栈里元素就是递增。如果是求左边第一个比自己小的元素，那么就是单调栈里元素就是递减。

使用单调栈主要有三个判断条件。

  • 当前遍历的元素T[i]小于栈顶元素T[st.top()]的情况
  • 当前遍历的元素T[i]等于栈顶元素T[st.top()]的情况
  • 当前遍历的元素T[i]大于栈顶元素T[st.top()]的情况
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
class Solution:
    def dailyTemperatures(self, temperatures: List[int]) -> List[int]:
        answer = [0]*len(temperatures)
        stack = [0]
        for i in range(1,len(temperatures)):
            # 情况一和情况二
            if temperatures[i]<=temperatures[stack[-1]]:
                stack.append(i)
            # 情况三
            else:
                while len(stack) != 0 and temperatures[i]>temperatures[stack[-1]]:
                    answer[stack[-1]]=i-stack[-1]
                    stack.pop()
                stack.append(i)

        return answer

解题思路：

  1. 单调栈的定义：单调栈是一种特殊的栈，它在任何时候都保持栈内的元素是单调的（递增或递减）。在这个问题中，我们需要找到每个气温后面第一个更高的气温，因此我们需要一个递增的单调栈。
  2. 栈的维护：遍历气温数组，对于每个气温，我们根据其与栈顶气温的关系来决定是否将其压入栈中或者弹出栈顶元素。
    • 如果当前气温大于栈顶气温，说明栈顶气温之后没有更高的气温，因此将栈顶气温的索引弹出，并更新结果数组中栈顶气温索引对应的值（等待天数）。
    • 如果当前气温小于或等于栈顶气温，将当前气温的索引压入栈中，因为可能存在更高的气温。
  3. 边界处理：在遍历过程中，如果栈为空或者当前气温小于栈顶气温，直接将当前索引压入栈中。这是因为栈为空时，第一个元素没有更高的气温，而当前气温小于栈顶气温时，我们还不知道后面是否有更高的气温。

关键点：

  1. 单调性：保持栈内的气温索引是递增的，这样才能确保栈顶元素的气温是当前已遍历过的气温中最小的，从而找到每个气温后面第一个更高的气温。
  2. 栈顶元素的处理：当遇到一个更高的气温时，栈顶元素及其下面的所有元素都找到了后续的第一个更高的气温，因此可以将它们从栈中弹出，并更新结果数组。
  3. 结果数组的初始化：结果数组应该初始化为0，因为如果某个元素的右边没有更高的气温，那么它对应的结果就是0。
  4. 时间复杂度：单调栈算法的时间复杂度为 O(n)，因为每个元素最多进栈和出栈一次，这比暴力解法的 O(n^2) 时间复杂度有显著提升。
  5. 空间复杂度：由于使用了额外的栈和结果数组，空间复杂度为 O(n)。

下一个更大元素 I

给你两个 没有重复元素 的数组 nums1 和 nums2 ，其中nums1 是 nums2 的子集。请你找出 nums1 中每个元素在 nums2 中的下一个比其大的值。nums1 中数字 x 的下一个更大元素是指 x 在 nums2 中对应位置的右边的第一个比 x 大的元素。如果不存在，对应位置输出 -1

示例 1，输入: nums1 = [4,1,2], nums2 = [1,3,4,2]，输出: [-1,3,-1]

  • result数组初始化应该为-1，题目说如果不存在对应位置就输出 -1 ，所以result数组如果某位置没有被赋值，那么就应该是是-1。
  • 我们应该遍历 nums2，在遍历nums2的过程中，我们要判断nums2[i]是否在nums1中出现过，因为最后是要根据nums1元素的下标来更新result数组。因为元素没有重复，所以可以用map来做映射了。根据数值快速找到下标，还可以判断nums2[i]是否在nums1中出现过。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution:
    def nextGreaterElement(self, nums1: List[int], nums2: List[int]) -> List[int]:
        result = [-1]*len(nums1)
        stack = [0]
        for i in range(1,len(nums2)):
            # 情况一情况二
            if nums2[i]<=nums2[stack[-1]]:
                stack.append(i)
            # 情况三
            else:
                while len(stack)!=0 and nums2[i]>nums2[stack[-1]]:
                    # in 是 Python 特有的写法，其他语言使用一个 map
                    if nums2[stack[-1]] in nums1:  
                        index = nums1.index(nums2[stack[-1]])
                        result[index]=nums2[i]
                    stack.pop()                 
                stack.append(i)
        return result

可以和下面的 Python 版本对比下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
    public int[] nextGreaterElement(int[] nums1, int[] nums2) {
        HashMap<Integer, Integer> map = new HashMap<>();
        for (int i = 0; i < nums1.length; i++) {
            map.put(nums1[i], i);
        }

        int[] res = new int[nums1.length];
        Stack<Integer> stack = new Stack<>();
        Arrays.fill(res, -1);

        for (int i = 0; i < nums2.length; i++) {
            while (!stack.isEmpty() && nums2[stack.peek()] < nums2[i]) {
                int pre = nums2[stack.pop()];
                if (map.containsKey(pre)) {
                    res[map.get(pre)] = nums2[i];
                }
            }
            stack.push(i);
        }

        return res;
    }
}

解题思路：

  1. 理解题目：给定两个数组 nums1 和 nums2，其中 nums1 是 nums2 的子集，要求找到 nums1 中每个元素在 nums2 中的下一个更大元素。如果不存在这样的元素，输出 -1。
  2. 使用哈希映射：由于 nums1 中的元素在 nums2 中的顺序可能会改变，我们首先需要建立一个映射，将 nums1 中的每个元素映射到 nums2 中的对应下标。这样我们就可以在后续的查找过程中快速定位。
  3. 单调栈的维护：使用一个单调递增栈来存储 nums2 中的元素的下标。栈中的元素应该保持递增顺序，这样我们可以在栈中找到比栈顶元素大的第一个元素。
  4. 遍历 nums2：遍历 nums2 数组，对于每个元素，根据其与栈顶元素的关系进行操作：
    • 如果当前元素大于栈顶元素，那么它就是栈顶元素在 nums2 中的下一个更大元素。更新结果数组，并弹出栈顶元素。
    • 如果当前元素小于或等于栈顶元素，将其下标压入栈中。
  5. 处理结果数组：在遍历结束后，如果结果数组中的某些位置没有被更新，那么这些位置的值应该保持为 -1，因为它们在 nums2 中没有更大的元素。

关键点：

  1. 哈希映射的建立：这是为了快速定位 nums1 中的元素在 nums2 中的位置，从而减少时间复杂度。
  2. 单调栈的性质：栈必须保持递增顺序，这样才能确保栈顶元素的下一个更大元素是正确的。
  3. 边界条件的处理：在处理 nums2 的边界元素时，需要特别注意，确保不会访问到栈中不存在的元素。
  4. 结果数组的初始化：结果数组应该初始化为 -1，以便在没有找到下一个更大元素时直接输出。
  5. 时间复杂度和空间复杂度：使用单调栈的方法可以将时间复杂度降低到 O(n)，其中 n 是 nums2 的长度。空间复杂度也是 O(n)，主要是因为我们需要额外的映射和结果数组。

下一个更大元素II

给定一个循环数组（最后一个元素的下一个元素是数组的第一个元素），输出每个元素的下一个更大元素。数字 x 的下一个更大的元素是按数组遍历顺序，这个数字之后的第一个比它更大的数，这意味着你应该循环地搜索它的下一个更大的数。如果不存在，则输出 -1。

示例 1，输入: [1,2,1]，输出: [2,-1,2]，解释: 第一个 1 的下一个更大的数是 2；数字 2 找不到下一个更大的数；第二个 1 的下一个最大的数需要循环搜索，结果也是 2

  • 方法一，可以直接把两个数组拼接在一起，然后使用单调栈求下一个最大值。这么做的确比较直观，但扩充nums数组相当于多了一个O(n)的操作。
  • 方法二，可以不扩充nums，而是在遍历的过程中使用 i % size 模拟走两遍 nums

java 版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
class Solution {
    public int[] nextGreaterElements(int[] nums) {
        //边界判断
        if(nums == null || nums.length <= 1) {
            return new int[]{-1};
        }
        int size = nums.length;
        int[] result = new int[size];//存放结果
        Arrays.fill(result,-1);//默认全部初始化为-1
        Stack<Integer> st= new Stack<>();//栈中存放的是nums中的元素下标
        for(int i = 0; i < 2*size; i++) {
            while(!st.empty() && nums[i % size] > nums[st.peek()]) {
                result[st.peek()] = nums[i % size];//更新result
                st.pop();//弹出栈顶
            }
            st.push(i % size);
        }
        return result;
    }
}

python 版本

1
2
3
4
5
6
7
8
9
10
class Solution:
    def nextGreaterElements(self, nums: List[int]) -> List[int]:
        dp = [-1] * len(nums)
        stack = []
        for i in range(len(nums)*2):
            while(len(stack) != 0 and nums[i%len(nums)] > nums[stack[-1]]):
                    dp[stack[-1]] = nums[i%len(nums)]
                    stack.pop()
            stack.append(i%len(nums))
        return dp

接雨水

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例 1：

输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]，输出：6，解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）

  • 首先单调栈是按照行方向来计算雨水

  • 找每个柱子左右两边第一个大于该柱子高度的柱子

  • 从栈头（元素从栈头弹出）到栈底的顺序应该是从小到大的顺序。因为一旦发现添加的柱子高度大于栈头元素了，此时就出现凹槽了，栈头元素就是凹槽底部的柱子，栈头第二个元素就是凹槽左边的柱子，而添加的元素就是凹槽右边的柱子。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
class Solution:
    def trap(self, height: List[int]) -> int:
        # 单调栈
        '''
        单调栈是按照 行 的方向来计算雨水
        从栈顶到栈底的顺序：从小到大
        通过三个元素来接水：栈顶，栈顶的下一个元素，以及即将入栈的元素
        雨水高度是 min(凹槽左边高度, 凹槽右边高度) - 凹槽底部高度
        雨水的宽度是 凹槽右边的下标 - 凹槽左边的下标 - 1（因为只求中间宽度）
        '''
        # stack储存index，用于计算对应的柱子高度
        stack = [0]
        result = 0
        for i in range(1, len(height)):
            # 情况一
            if height[i] < height[stack[-1]]:
                stack.append(i)

            # 情况二
            # 当当前柱子高度和栈顶一致时，左边的一个是不可能存放雨水的，所以保留右侧新柱子
            # 需要使用最右边的柱子来计算宽度
            elif height[i] == height[stack[-1]]:
                stack.pop()
                stack.append(i)

            # 情况三
            else:
                # 抛出所有较低的柱子
                while stack and height[i] > height[stack[-1]]:
                    # 栈顶就是中间的柱子：储水槽，就是凹槽的地步
                    mid_height = height[stack[-1]]
                    stack.pop()
                    if stack:
                        right_height = height[i]
                        left_height = height[stack[-1]]
                        # 两侧的较矮一方的高度 - 凹槽底部高度
                        h = min(right_height, left_height) - mid_height
                        # 凹槽右侧下标 - 凹槽左侧下标 - 1: 只求中间宽度
                        w = i - stack[-1] - 1
                        # 体积：高乘宽
                        result += h * w
                stack.append(i)
        return result
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
from typing import List


class Solution:
    def trap(self, height: List[int]) -> int:
        stack = [0]
        result = 0
        for i in range(1, len(height)):
            # 情况一
            if height[i] < height[stack[-1]]:
                stack.append(i)
                print(f"当前i: {i}, 元素 {height[i]} 小于栈顶元素，元素入栈, 栈为: {stack}")

            elif height[i] == height[stack[-1]]:
                stack.pop()
                stack.append(i)
                print(f"当前i: {i}, 元素 {height[i]} 等于栈顶元素，stack 先出栈，元素后入栈, 栈为: {stack}")

            else:
                while stack and height[i] > height[stack[-1]]:
                    mid_height = height[stack[-1]]
                    stack.pop()
                    print(f"当前i: {i}, 元素 {height[i]} 大于栈顶元素，stack 出栈，栈为: {stack}")

                    if stack:
                        right_height = height[i]
                        left_height = height[stack[-1]]
                        h = min(right_height, left_height) - mid_height
                        w = i - stack[-1] - 1
                        result += h * w
                        print(f"出栈后栈不为空，左边柱子高为: {left_height}, 右边柱子高为: {right_height}，最小高为:{h}，宽为: {w}, 面积为: {w}, 总面积为: {result}")
                    else:
                        print("出栈后栈为空")
                stack.append(i)
                print(f"都处理完了，当前 i:{i} 入栈: {stack}")
        return result


if __name__ == '__main__':
    s = Solution()
    s.trap([0, 1, 0, 2, 1, 0, 1, 3, 2, 1, 2, 1])

   
"""
当前i: 1, 元素 1 大于栈顶元素，stack 出栈，栈为: []
出栈后栈为空
都处理完了，当前 i:1 入栈: [1]
当前i: 2, 元素 0 小于栈顶元素，元素入栈, 栈为: [1, 2]
当前i: 3, 元素 2 大于栈顶元素，stack 出栈，栈为: [1]
出栈后栈不为空，左边柱子高为: 1, 右边柱子高为: 2，最小高为:1，宽为: 1, 面积为: 1, 总面积为: 1
当前i: 3, 元素 2 大于栈顶元素，stack 出栈，栈为: []
出栈后栈为空
都处理完了，当前 i:3 入栈: [3]
当前i: 4, 元素 1 小于栈顶元素，元素入栈, 栈为: [3, 4]
当前i: 5, 元素 0 小于栈顶元素，元素入栈, 栈为: [3, 4, 5]
当前i: 6, 元素 1 大于栈顶元素，stack 出栈，栈为: [3, 4]
出栈后栈不为空，左边柱子高为: 1, 右边柱子高为: 1，最小高为:1，宽为: 1, 面积为: 1, 总面积为: 2
都处理完了，当前 i:6 入栈: [3, 4, 6]
当前i: 7, 元素 3 大于栈顶元素，stack 出栈，栈为: [3, 4]
出栈后栈不为空，左边柱子高为: 1, 右边柱子高为: 3，最小高为:0，宽为: 2, 面积为: 2, 总面积为: 2
当前i: 7, 元素 3 大于栈顶元素，stack 出栈，栈为: [3]
出栈后栈不为空，左边柱子高为: 2, 右边柱子高为: 3，最小高为:1，宽为: 3, 面积为: 3, 总面积为: 5
当前i: 7, 元素 3 大于栈顶元素，stack 出栈，栈为: []
出栈后栈为空
都处理完了，当前 i:7 入栈: [7]
当前i: 8, 元素 2 小于栈顶元素，元素入栈, 栈为: [7, 8]
当前i: 9, 元素 1 小于栈顶元素，元素入栈, 栈为: [7, 8, 9]
当前i: 10, 元素 2 大于栈顶元素，stack 出栈，栈为: [7, 8]
出栈后栈不为空，左边柱子高为: 2, 右边柱子高为: 2，最小高为:1，宽为: 1, 面积为: 1, 总面积为: 6
都处理完了，当前 i:10 入栈: [7, 8, 10]
当前i: 11, 元素 1 小于栈顶元素，元素入栈, 栈为: [7, 8, 10, 11]
"""

柱状图中最大的矩形

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。求在该柱状图中，能够勾勒出来的矩形的最大面积。

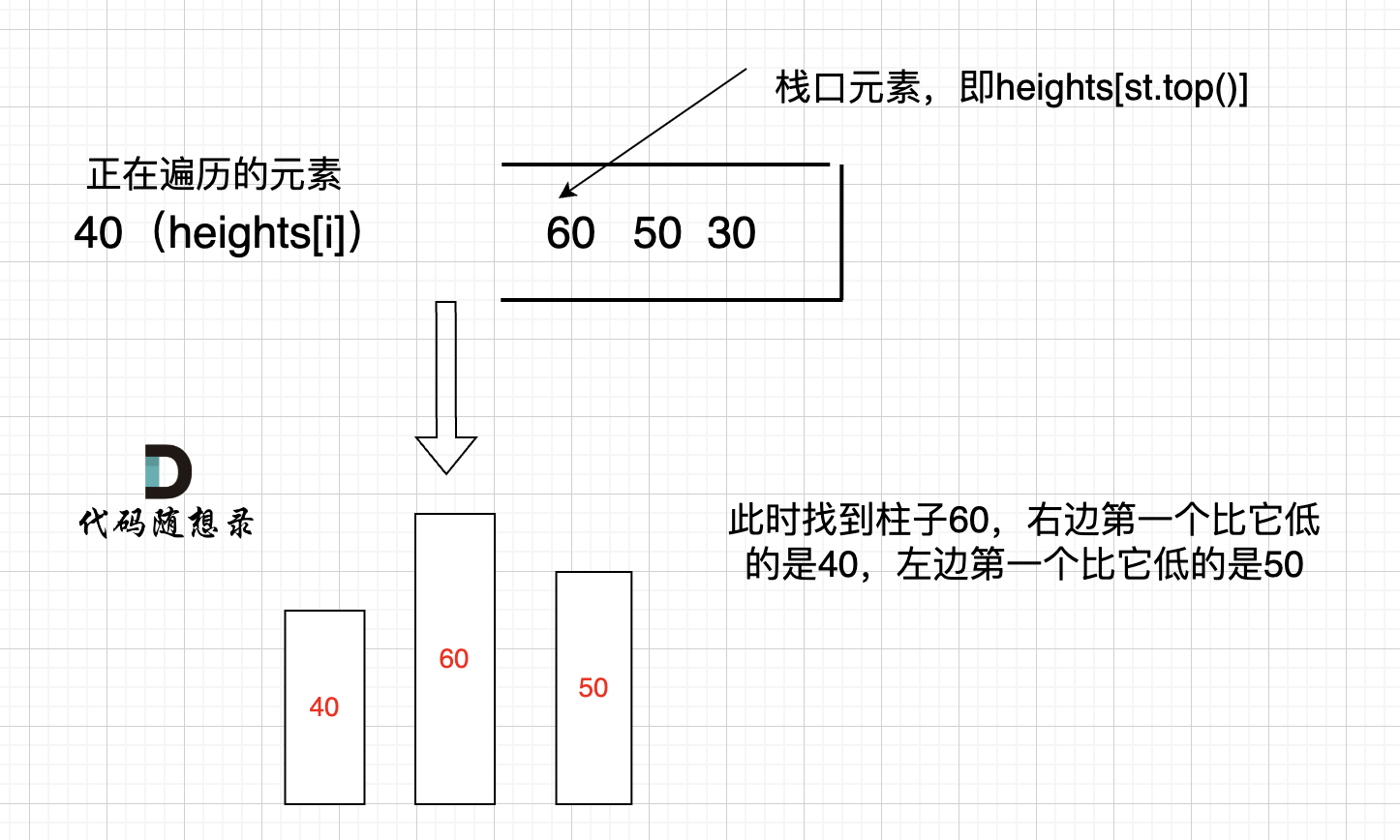
  • 接雨水是找每个柱子左右两边第一个大于该柱子高度的柱子，而本题是找每个柱子左右两边第一个小于该柱子的柱子

  • 接雨水的单调栈从栈头（元素从栈头弹出）到栈底的顺序应该是从小到大的顺序。那么因为本题是要找每个柱子左右两边第一个小于该柱子的柱子，所以从栈头（元素从栈头弹出）到栈底的顺序应该是从大到小的顺序。

  • 栈顶和栈顶的下一个元素以及要入栈的三个元素组成了我们要求最大面积的高度和宽度

  • 我们需要在 height数组前后各加一个元素0。因为单调递减栈是当当前元素小于栈顶元素时才做逻辑，如果数组本身就是升序的，例如[2,4,6,8]，那么入栈之后 都是单调递减，即一直在入栈却没有出栈的逻辑。所以需要在原数组结尾加一个0，这样入栈就不是一直单调递减了。同样，如果数组是递减的，那么栈中的元素会一直单调递增，也无法计算出结果。

    在处理柱状图时，如果数组是完全递增或完全递减的，那么在计算过程中可能会遇到特殊情况，导致计算逻辑不完整。例如，如果数组是递增的，那么在处理过程中，栈中的元素会一直单调递减，而没有机会计算出最大矩形的面积。同样，如果数组是递减的，那么栈中的元素会一直单调递增，也无法计算出结果。

    通过在数组的前后各加上一个0，我们可以确保在处理数组的第一个和最后一个元素时，它们都能找到一个小于它们的柱子（即数组首尾的0）。这样，无论数组的初始状态如何，我们都可以保证单调栈的逻辑能够完整执行，从而计算出所有可能的最大矩形面积

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
# 单调栈
class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:
        # Monotonic Stack
        '''
        找每个柱子左右侧的第一个高度值小于该柱子的柱子
        单调栈：栈顶到栈底：从大到小（每插入一个新的小数值时，都要弹出先前的大数值）
        栈顶，栈顶的下一个元素，即将入栈的元素：这三个元素组成了最大面积的高度和宽度
        情况一：当前遍历的元素heights[i]大于栈顶元素的情况
        情况二：当前遍历的元素heights[i]等于栈顶元素的情况
        情况三：当前遍历的元素heights[i]小于栈顶元素的情况
        '''

        # 输入数组首尾各补上一个0（与42.接雨水不同的是，本题原首尾的两个柱子可以作为核心柱进行最大面积尝试
        heights.insert(0, 0)
        heights.append(0)
        stack = [0]
        result = 0
        for i in range(1, len(heights)):
            # 情况一
            # 单调递减栈，当发现当前元素大于栈顶元素时则入栈（入栈后，栈里的元素才是单调递减）
            if heights[i] > heights[stack[-1]]:
                stack.append(i)
            # 情况二
            elif heights[i] == heights[stack[-1]]:
                stack.pop()
                stack.append(i)
            # 情况三
            else:
                # 抛出所有较高的柱子
                # 当栈不为空，且当前元素小于栈顶元素时。说明找到了栈顶元素左右两边的第一个小的元素。
                while stack and heights[i] < heights[stack[-1]]:
                    # 栈顶就是中间的柱子，主心骨
                    mid_index = stack[-1]  # 记录栈顶元素的下标
                    stack.pop()
                    if stack:
                        left_index = stack[-1]  # 栈顶元素左边矮的柱子的下标
                        right_index = i  # 栈顶元素右边矮的柱子的下标
                        width = right_index - left_index - 1  # 宽
                        height = heights[mid_index]  # 高
                        result = max(result, width * height)
                stack.append(i)
        return result
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
# 单调栈
from typing import List


class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:
        heights.insert(0, 0)
        heights.append(0)
        stack = [0]
        result = 0
        for i in range(1, len(heights)):
            if heights[i] > heights[stack[-1]]:
                print(f"当前 i: {i}, 元素: {heights[i]} 大于栈顶元素:{heights[stack[-1]]}")
                stack.append(i)
                print(f"元素入栈，栈为: {stack}")

            elif heights[i] == heights[stack[-1]]:
                print(f"当前 i: {i}, 元素: {heights[i]} 等于栈顶元素{heights[stack[-1]]}")
                stack.pop()
                stack.append(i)
                print(f"元素先出栈后入栈，栈为: {stack}")

            else:
                while stack and heights[i] < heights[stack[-1]]:
                    print(f"当前 i: {i}, 元素: {heights[i]} 小于栈顶元素 {heights[stack[-1]]}")

                    # 栈顶就是中间的柱子，主心骨
                    mid_index = stack[-1]  # 记录栈顶元素的下标
                    stack.pop()
                    print(f"元素出栈，栈为: {stack}")

                    if stack:
                        print("元素出栈后栈不为空")
                        left_index = stack[-1]  # 栈顶元素左边矮的柱子的下标
                        right_index = i  # 栈顶元素右边矮的柱子的下标
                        width = right_index - left_index - 1  # 宽
                        height = heights[mid_index]  # 高
                        print(f"柱子右下标为: {right_index}, 左下标为: {left_index}, 宽为: {width}")
                        print(f"当前柱子下标为: {mid_index}, 高为: {height}, 当前面积为: {width * height}")
                        result = max(result, width * height)
                        print(f"取最大面积后，最大面积为: {result}")
                    else:
                        print(f"元素出栈后栈为空")

                stack.append(i)
        return result


if __name__ == '__main__':
    s = Solution()
    s.largestRectangleArea([2, 1, 5, 6, 2, 3])

    
"""
当前 i: 1, 元素: 2 大于栈顶元素:0
元素入栈，栈为: [0, 1]
当前 i: 2, 元素: 1 小于栈顶元素 2
元素出栈，栈为: [0]
元素出栈后栈不为空
柱子右下标为: 2, 左下标为: 0, 宽为: 1
当前柱子下标为: 1, 高为: 2, 当前面积为: 2
取最大面积后，最大面积为: 2
当前 i: 3, 元素: 5 大于栈顶元素:1
元素入栈，栈为: [0, 2, 3]
当前 i: 4, 元素: 6 大于栈顶元素:5
元素入栈，栈为: [0, 2, 3, 4]
当前 i: 5, 元素: 2 小于栈顶元素 6
元素出栈，栈为: [0, 2, 3]
元素出栈后栈不为空
柱子右下标为: 5, 左下标为: 3, 宽为: 1
当前柱子下标为: 4, 高为: 6, 当前面积为: 6
取最大面积后，最大面积为: 6
当前 i: 5, 元素: 2 小于栈顶元素 5
元素出栈，栈为: [0, 2]
元素出栈后栈不为空
柱子右下标为: 5, 左下标为: 2, 宽为: 2
当前柱子下标为: 3, 高为: 5, 当前面积为: 10
取最大面积后，最大面积为: 10
当前 i: 6, 元素: 3 大于栈顶元素:2
元素入栈，栈为: [0, 2, 5, 6]
当前 i: 7, 元素: 0 小于栈顶元素 3
元素出栈，栈为: [0, 2, 5]
元素出栈后栈不为空
柱子右下标为: 7, 左下标为: 5, 宽为: 1
当前柱子下标为: 6, 高为: 3, 当前面积为: 3
取最大面积后，最大面积为: 10
当前 i: 7, 元素: 0 小于栈顶元素 2
元素出栈，栈为: [0, 2]
元素出栈后栈不为空
柱子右下标为: 7, 左下标为: 2, 宽为: 4
当前柱子下标为: 5, 高为: 2, 当前面积为: 8
取最大面积后，最大面积为: 10
当前 i: 7, 元素: 0 小于栈顶元素 1
元素出栈，栈为: [0]
元素出栈后栈不为空
柱子右下标为: 7, 左下标为: 0, 宽为: 6
当前柱子下标为: 2, 高为: 1, 当前面积为: 6
取最大面积后，最大面积为: 10
"""